 |
 |
Konsep Himpunan untuk Memecahkan Masalah
Uraian
Baiklah peserta didik sekalian, apakah kalian sudah menyelesaikan kuis tadi dengan baik? Apakah kalian dapat memahami konsep himpunan dan diagram Venn yang ada pada kuis tersebut? Bagus! Berarti kalian sudah memahaminya, jika belum kalian dapat mengulang kembali kuis tersebut.
Untuk lebih memahami dan mendalami konsep himpunan dan diagram Venn serta mengetahui manfaatnya yang dapat kita pergunakan untuk memecahkan masalah dalam kehidupan sehari-hari, marilah kita sama-sama mempelajari lebih jauh lagi.
Pada kehidupan sehari-hari kita sering menemukan masalah seperti berikut : Dalam suatu kelompok bermain sebanyak 20 anak, ternyata 14 anak menyukai permainan bola sepak, 12 anak menyukai permainan lompat tali. Berapa anak yang menyukai kedua permainan tersebut? Berapa anak yang tidak menyukai kedua permainan tersebut? Berapa anak yang menyukai permainan bola sepak atau lompat tali? Berapa anak yang hanya menyukai permainan bola sepak saja? Berapa anak yang hanya menyukai permainan lompat tali saja?
Bagaimana menyelesaikan masalah tersebut? Apakah kalian mengerti? Jika belum, mari kita simak langkah-langkah dalam menyelesaikan masalah tersebut!
Langkah 1:
Untuk menyelesaikan permasalahan tersebut, kita perlu mengubah pernyataan-pernyataan yang ada dalam masalah tersebut (soal cerita) ke dalam bentuk matematika. Bagaimana caranya? Mari kalian simak baik-baik!
“Dalam suatu kelompok bermain sebanyak 20 anak”. Itu berarti himpunan Semestanya ada 20 atau n(S) = 20.
Kalimat berikutnya, “ternyata 14 anak menyukai permainan bola sepak”, Anak yang menyukai permainan sepak bola, kita misalkan himpunan A, Itu berarti himpunan A ada 14 atau n(A) = 14.
Kalimat berikutnya, “12 anak menyukai permainan lompat tali.”, Anak yang menyukai permainan lompat tali, kita misalkan himpunan B, Itu berarti himpunan B ada 12 atau n(B) = 12.
Kalimat pertanyaan pertama, “Berapa anak yang menyukai kedua permainan tersebut?”, kalimat pertanyaan itu berarti berapa n(A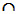
B)?
Kalimat pertanyaan kedua, “Berapa anak yang tidak menyukai kedua permainan tersebut?”, kalimat pertanyaan itu berarti berapa n(A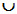
B)`?
Kalimat pertanyaan ketiga, “Berapa anak yang menyukai permainan bola sepak atau lompat tali?”, kalimat pertanyaan itu berarti berapa n(A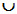 B)?
Kalimat pertanyaan keempat, “Berapa anak yang hanya menyukai permainan bola sepak saja?”, kalimat pertanyaan itu berarti berapa n(A - B)?
Kalimat pertanyaan kelima, “Berapa anak yang hanya menyukai permainan lompat talii saja?”, kalimat pertanyaan itu berarti berapa n(B - A)?
Nah, sekarang kita sudah mempunyai kalimat (lambang) matematikanya, yaitu :
Diketahui : n(S) = 20
n(A) = 14
n(B) = 12
Ditanya : 1. n (A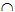
B)
2. n (A
B)`
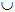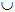3. n (A B)
4. n (A - B)
5. n (B - A)
Langkah 2:
Setelah pada langkah pertama kita membuat kalimat (lambang) matematika, maka pada langkah keduanya kita membuat diagram Venn. Sesuai dengan langkah pertama, karena ada dua himpunan yaitu himpunan A dan himpunan B, berarti kita mempunyai dua kurva tertutup (lingkaran) yaitu kurva tertutup A dan kurva tertutup B, dimana keadaan kedua kurva tertutup tersebut saling berpotongan, karena ada anak yang menyukai kedua permainan tersebut.
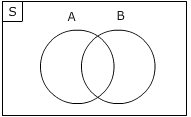
Langkah 3:
Setelah mengetahui keadaan kedua kurva tertutup tersebut, pada langkah ketiga, kita masukkan nilai-nilai dari diagram Venn tersebut (mengisi diagram Venn). Dalam mengisi diagram Venn yang pertama kali diisi/dimasukkan adalah nilai irisan/perpotongan dari kurva tertutup A dan kurva tertutup B, karena nilai irisan/perpotongan dari kurva tertutup A dan kurva tertutup B belum ada, maka kita misalkan nilainya x.
Langkah 4:
Pada langkah keempat kita menentukan nilai x, dengan membuat sebuah persamaan, yaitu :
n(S) = (14 - x) + x + (12 - x) → perhatikan diagram Venn
20 = (14 - x) + x + (12 - x)
20 = 26 - x
x = 26 - 20
x = 6
Setelah mendapatkan nilai x, kita isi/masukkan kembali nilai-nilai tersebut ke dalam diagram Venn.
Langkah 5:
Pada langkah kelima kita jawab pertanyaan-pertanyaannya sesuai dengan gambar diagram Venn yang sudah kita buat.
Pertanyaan – Pertanyaan : 1. n (A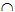 B)
2. n (A B)`
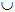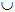3. n (A B)
4. n (A - B)
5. n (B - A)
Penyelesaian :
1. n (A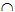 B) = 6, karena nilai irisan/perpotongan kurva A dan Kurva B adalah 6.
Jadi anak yang menyukai kedua permainan tersebut ada 6 orang.
2. n (A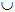 B)`= 0, karena tidak ada nilai di luar kurva A dan Kurva B.
Jadi anak yang tidak menyukai kedua permainan tersebut ada 0 orang (tidak ada).
3. n (A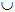 B) = 8 + 6 + 6 = 20, karena nilai yang berada di dalam kurva A atau Kurva B adalah 8,
6 dan 6.
Jadi anak yang menyukai permainan bola sepak atau lompat tali ada 20 orang.
4. n (A - B) = 14 – 6 = 8 , karena nilai yang berada di dalam kurva A saja adalah 8.
Jadi anak yang hanya menyukai permainan bola sepak saja ada 8 orang .
5. n (B - A)= 12 – 6 = 6 , karena nilai yang berada di dalam kurva B saja adalah 6.
Jadi anak yang hanya menyukai permainan lompat tali saja ada 6 orang.
Peserta didik sekalian, apakah kalian sudah paham dengan penjelasan dan penyelesaian contoh soal di atas? Apakah kalian dapat memahami bagaimana cara memecahkan masalah dalam kehidupan sehari-hari dengan menggunakan konsep himpunan? Bagus, nah untuk mengetahui apakah kalian benar-benar memahami materi ini silakan kalian coba simulasi di bawah ini, selamat mencoba!
Untuk lebih memahami dan mendalami konsep himpunan dan diagram Venn serta mengetahui manfaatnya yang dapat kita pergunakan untuk memecahkan masalah dalam kehidupan sehari-hari, marilah kita sama-sama mempelajari lebih jauh lagi.
Pada kehidupan sehari-hari kita sering menemukan masalah seperti berikut : Dalam suatu kelompok bermain sebanyak 20 anak, ternyata 14 anak menyukai permainan bola sepak, 12 anak menyukai permainan lompat tali. Berapa anak yang menyukai kedua permainan tersebut? Berapa anak yang tidak menyukai kedua permainan tersebut? Berapa anak yang menyukai permainan bola sepak atau lompat tali? Berapa anak yang hanya menyukai permainan bola sepak saja? Berapa anak yang hanya menyukai permainan lompat tali saja?
Bagaimana menyelesaikan masalah tersebut? Apakah kalian mengerti? Jika belum, mari kita simak langkah-langkah dalam menyelesaikan masalah tersebut!
Langkah 1:
Untuk menyelesaikan permasalahan tersebut, kita perlu mengubah pernyataan-pernyataan yang ada dalam masalah tersebut (soal cerita) ke dalam bentuk matematika. Bagaimana caranya? Mari kalian simak baik-baik!
“Dalam suatu kelompok bermain sebanyak 20 anak”. Itu berarti himpunan Semestanya ada 20 atau n(S) = 20.
Kalimat berikutnya, “ternyata 14 anak menyukai permainan bola sepak”, Anak yang menyukai permainan sepak bola, kita misalkan himpunan A, Itu berarti himpunan A ada 14 atau n(A) = 14.
Kalimat berikutnya, “12 anak menyukai permainan lompat tali.”, Anak yang menyukai permainan lompat tali, kita misalkan himpunan B, Itu berarti himpunan B ada 12 atau n(B) = 12.
Kalimat pertanyaan pertama, “Berapa anak yang menyukai kedua permainan tersebut?”, kalimat pertanyaan itu berarti berapa n(A
B)? Kalimat pertanyaan kedua, “Berapa anak yang tidak menyukai kedua permainan tersebut?”, kalimat pertanyaan itu berarti berapa n(A
B)`? Kalimat pertanyaan ketiga, “Berapa anak yang menyukai permainan bola sepak atau lompat tali?”, kalimat pertanyaan itu berarti berapa n(A
B)? Kalimat pertanyaan keempat, “Berapa anak yang hanya menyukai permainan bola sepak saja?”, kalimat pertanyaan itu berarti berapa n(A - B)?
Kalimat pertanyaan kelima, “Berapa anak yang hanya menyukai permainan lompat talii saja?”, kalimat pertanyaan itu berarti berapa n(B - A)?
Nah, sekarang kita sudah mempunyai kalimat (lambang) matematikanya, yaitu :
Diketahui : n(S) = 20
n(A) = 14
n(B) = 12
Ditanya : 1. n (A
B)2. n (A
B)`3. n (A
B)4. n (A - B)
5. n (B - A)
Langkah 2:
Setelah pada langkah pertama kita membuat kalimat (lambang) matematika, maka pada langkah keduanya kita membuat diagram Venn. Sesuai dengan langkah pertama, karena ada dua himpunan yaitu himpunan A dan himpunan B, berarti kita mempunyai dua kurva tertutup (lingkaran) yaitu kurva tertutup A dan kurva tertutup B, dimana keadaan kedua kurva tertutup tersebut saling berpotongan, karena ada anak yang menyukai kedua permainan tersebut.
Langkah 3:
Setelah mengetahui keadaan kedua kurva tertutup tersebut, pada langkah ketiga, kita masukkan nilai-nilai dari diagram Venn tersebut (mengisi diagram Venn). Dalam mengisi diagram Venn yang pertama kali diisi/dimasukkan adalah nilai irisan/perpotongan dari kurva tertutup A dan kurva tertutup B, karena nilai irisan/perpotongan dari kurva tertutup A dan kurva tertutup B belum ada, maka kita misalkan nilainya x.
Langkah 4:
Pada langkah keempat kita menentukan nilai x, dengan membuat sebuah persamaan, yaitu :
n(S) = (14 - x) + x + (12 - x) → perhatikan diagram Venn
20 = (14 - x) + x + (12 - x) 20 = 26 - x x = 26 - 20 x = 6Setelah mendapatkan nilai x, kita isi/masukkan kembali nilai-nilai tersebut ke dalam diagram Venn.
Langkah 5:
Pada langkah kelima kita jawab pertanyaan-pertanyaannya sesuai dengan gambar diagram Venn yang sudah kita buat.
Pertanyaan – Pertanyaan : 1. n (A
B)2. n (A
B)`3. n (A
B)4. n (A - B)
5. n (B - A)
Penyelesaian :
1. n (A
B) = 6, karena nilai irisan/perpotongan kurva A dan Kurva B adalah 6.Jadi anak yang menyukai kedua permainan tersebut ada 6 orang.
2. n (A
B)`= 0, karena tidak ada nilai di luar kurva A dan Kurva B.Jadi anak yang tidak menyukai kedua permainan tersebut ada 0 orang (tidak ada).
3. n (A
B) = 8 + 6 + 6 = 20, karena nilai yang berada di dalam kurva A atau Kurva B adalah 8, 6 dan 6.
Jadi anak yang menyukai permainan bola sepak atau lompat tali ada 20 orang.
4. n (A - B) = 14 – 6 = 8 , karena nilai yang berada di dalam kurva A saja adalah 8.
Jadi anak yang hanya menyukai permainan bola sepak saja ada 8 orang .
5. n (B - A)= 12 – 6 = 6 , karena nilai yang berada di dalam kurva B saja adalah 6.
Jadi anak yang hanya menyukai permainan lompat tali saja ada 6 orang.
Peserta didik sekalian, apakah kalian sudah paham dengan penjelasan dan penyelesaian contoh soal di atas? Apakah kalian dapat memahami bagaimana cara memecahkan masalah dalam kehidupan sehari-hari dengan menggunakan konsep himpunan? Bagus, nah untuk mengetahui apakah kalian benar-benar memahami materi ini silakan kalian coba simulasi di bawah ini, selamat mencoba!
