Penyelesaian Masalah Barisan dan Deret Geometri

Ingat apa yang dimaksud dengan barisan dan deret geometri? Ya, barisan dan deret geometri adalah barisan bilangan yang mempunyai perbandingan atau rasio yang selalu tetap. Misal barisan bilangan U1, U2, U3, U4, U5, U6, …, Un memiliki perbandingan yang selalu tetap jika   

Dalam barisan geometri U₁, U₂, U₃, U₄, ……, U_n dengan suku awal (a) = U₁ dan nilai rasio = r, dan r ≠ 1 berlaku rumus suku ke-n (U_n) sebagai berikut:

Un = a x rn – 1

Dalam deret geometri U₁, U₂, U₃, U₄, ……, U_n dengan suku awal (a) = U₁ dan nilai rasio = r, berlaku rumus jumlah n suku pertama (S_n) sebagai berikut:

Nah sekarang bagaimana pengetahuan tentang barisan dan deret geometri tersebut dapat kalian gunakan untuk menyelesaikan masalah-masalah sehari-hari yang berkaitan dengan barisan dan deret bilangan geometri? Perhatikan pada gambar berikut.



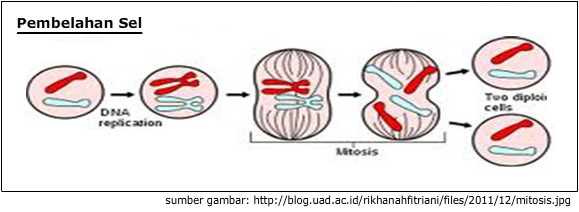
Pada gambar nampak proses pembelahan sel dari satu sel menjadi dua sel dalam setiap jangka waktu tertentu. Pada proses pembelahan sel tersebut setiap 12 menit membelah menjadi dua sel, demikian seterusnya. Dapatkah kalian menentukan ada berapa banyak sel yang terjadi setelah 2 jam?

Permasalahan tersebut dapat diselesaikan dengan barisan geometri. Barisan bilangan  geometri adalah barisan bilangan yang mempunyai rasio tetap antar setiap sukunya.
Barisan bilangan yang terjadi pada proses pembelahan sel adalah:

1, 2, 4, 8, 16, 32, ……………
Suku pertama (a) = 1
Rasio (r) = 2

Proses pembelahan yang terjadi setelah 2 jam (120 menit) adalah 120 menit : 12 menit = 10 kali pembelahan, berarti banyaknya suku pada barisan tersebut ada sebanyak 10 + 1 = 11 suku.
Banyaknya sel setelah 10 kali pembelahan = U11. Penyelesaiannya menggunakan rumus
Un = a.r^{n -1}
U11 = 1. 2^{11 - 1}
      = 2¹⁰
      = 1.024

Banyaknya sel yang terjadi setalah 120 menit adalah 1.024 sel.

Contoh Soal: