Baiklah peserta didik sekalian, apakah kalian sudah menyelesaikan kuis tadi dengan baik? Apakah kalian dapat memahami pengertian sebangun antara dua bidang datar yang ada pada kuis tersebut? Bagus! Berarti kalian sudah mulai memahaminya, jika belum kalian dapat mengulang kembali kuis itu.
Untuk lebih memahami dan mendalami mengenai pengertian kesebangunan dan mengetahui manfaat yang dapat kita pergunakan dalam kegiatan kita sehari-hari, marilah kita sama-sama mempelajari materi kesebangunan bidang datar ini lebih jauh lagi.
Coba kalian perhatikan animasi berikut. Pada gambar bidang berpetak berikut terdapat persegi panjang ABCD berukuran panjang 3 satuan dan lebar 2 satuan, serta persegi panjang PQRS berukuran panjang 6 satuan dan lebar 4 satuan.

Bisakah kalian menunjukkan pasangan sisi-sisi yang bersesuaian letaknya antara kedua persegi panjang tersebut? Kliklah pada tombol  play.

 

 Pasangan sisi-sisi yang bersesuaian pada kedua persegi panjang tersebut adalah : 
AB dengan PQ, BC dengan QR, CD dengan RS, dan AD dengan PS
Berapakah perbandingan ukuran sisi-sisi yang bersesuaian tersebut? Benar, perbandingan ukuran panjang kedua persegi panjang itu adalah:

AB = CD = 3 = 1
PQ    RS    6    2

 Perbandingan ukuran lebar kedua kedua persegi panjang adalah:

AD  = BC = 2 = 1
PS     QR    4    2

Perbandingan ukuran panjang dan lebar kedua persegi panjang ABCD dan PQRS adalah
sama atau senilai, yaitu:

 AB = CD = AD = BC = 1
PQ     RS    PS     QR    2

 

Bagaimanakah ukuran sudut-sudut yang bersesuaiannya?Sudut-sudut yang bersesuaian sama besar, yaitu :

Ð A = Ð P = 90^o,  Ð B =  Ð Q = 90^o, Ð C =  Ð R = 90^o, dan  Ð D = Ð S = 90^o

 Dapatkah kalian simpulkan dari animasi tadi? Coba kalian simpulkan! Benar, karena kedua persegi panjang ABCD dan PQRS mempunyai:
a. perbandingan sisi-sisi yang bersesuaian sama
b. besar sudut-sudut yang bersesuaian sama

maka kedua persegi panjang tersebut dikatakan sebangun. Notasinya 

Bagaimana peserta didik sekalian? Sudah dapat memahami tentang pengertian sebangun? Jika ingin lebih jelas, kita lihat animasi berikut ini. Pada gambar bidang berpetak berikut terdapat trapesium JKLM dengan JK = 4 satuan, KL =2 satuan dan LM = 2 satuan, serta  trapesium STUV dengan ST = 8 satuan, TU = 4 satuan dan UV = 4 satuan. Bisa kalian tunjukkan pasangan sisi-sisi yang bersesuaiannya? Coba kalian klik tombol play !

 

 

Pasangan sisi-sisi yang bersesuaian pada kedua trapesium adalah :  JK dengan ST, KL dengan TU, LM dengan UV, dan JM dengan SV
Bagaimana perbandingan ukuran sisi-sisi yang bersesuaian tersebut? Benar, perbandingannya adalah sebagai berikut:

 

Perbandingan sisi-sisi yang bersesuaian adalah sama atau senilai. Bagaimana dengan besar sudut-sudut yang bersesuaian?

Bagaimana kesimpulan kalian? Benar, karena kedua trapesium siku-siku  JKLM dan STUV mempunyai:
a. perbandingan sisi-sisi yang bersesuaian sama
b. besar sudut-sudut yang bersesuaian sama

maka kedua trapesium tersebut tersebut dikatakan sebangun. Notasinya :

Kesimpulan :
Dua bidang datar dikatakan sebangun jika memenuhi dua syarat berikut :
1. Perbandingan panjang sisi-sisi yang bersesuaian sama
2. Besar sudut-sudut yang bersesuaian sama

Selidikilah kedua persegi panjang ABCD dan JKLM pada gambar, apakah sebangun ?

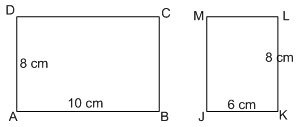
Untuk menentukan apakah kedua persegi panjang tersebut sebangun, kalian tentukan perbandingan panjang sisi-sisi yang bersesuaian apakah mempunyai perbandingan senilai atau tidak.

AB = 10 = 5   sedang  AD = 8 = 4
 KL     8     4                JK   6   3

Karena perbandingan sisi-sisi yang bersesuaian tidak sama atau tidak senilai, maka persegi panjang ABCD tidak sebangun dengan persegi panjang JKLM.

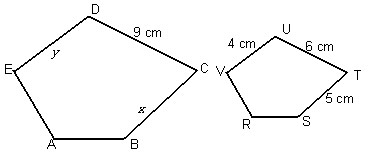
Segibanyak ABCDE dan RSTUV sebangun. Jika CD = 9 cm, ST = 5 cm, TU = 6 cm dan UV = 4 cm. Tentukanlah panjang BC dan DE?
Bagaimana menurutmu?

Karena kedua segibanyak sebangun, maka mempunyai perbandingan sisi-sisi yang bersesuaian yang sama atau senilai.
Menentukan panjang BC, perbandingan yang digunakan yaitu:

CD = BC
TU    ST

 9    =  x
 6        5

Dengan perkalian silang, didapat:


6x = 9 x 5
6x = 45
x   = 45
         6
x   = 7 1  
           2                                   
Jadi panjang BC adalah 7 1
                                  2       

Menentukan panjang DE, perbandingan yang digunakan yaitu:

CD =  DE
TU      UV

9   =   y
6        4

Dengan perkalian silang, didapat:
 6y = 9 x 4
 6y = 36
   y = 45
          6
  y = 6 jadi panjang BC adalah 6cm

 

Perhatikan lukisan pemandangan pada sebuah pigura. Panjang lukisan 80 cm, lebar lukisan 60 cm dan panjang pigura 100 cm. Tentukan lebar pigura tersebut jika lukisan dan piguranya sebangun!

Bagaimanakah kalian menentukan lebar pigura tersebut? Kalian ingin tahu jawabannya? 
Benar, karena bentuk lukisan dan pigura sebangun maka memiliki perbandingan yang sama atau senilai, yaitu:

panjang lukisan  = lebar lukisan
panjang pigura       lebar pigura

80  = 60                          jika misal lebar pigura = p maka,
100   lebar pigura        

4  = 60
5      p
 4 x p = 5 x 60
     4p = 300

       p= 300

      p = 300
             4

  p = 75 jadi lebar pigura adalah 75

Peserta didik sekalian, apakah kalian paham dengan penjelasan dan penyelesianan beberapa contoh soal tadi? Bagus. Nah untuk mengetahui apakah kalian benar-benar memahami materi ini silahkan kalian mengerjakan soal-soal pada latihan berikut ini. Selamat mengerjakan! Semoga kalian sukses.