Sumber Belajar

Kesebangunan

Segitiga-segitiga yang diketahui ukuran ketiga sisinya

Segitiga-segitiga yang sebangun
Peserta didik sekalian, apakah kalian sudah mengerjakan latihan tentang kesebangunan bidang datar pada latihan sebelumnya? Mudah, bukan? Jika kalian belum tuntas mengerjakan latihannya, kalian coba kembali mengerjakannya. Sampai kalian benar-benar tuntas.

Nah sekarang kalian akan lebih jauh lagi memahami kesebangunan khusus pada segitiga. Kalian masih ingat sifat-sifat segitiga? Ya benar, segitiga merupakan bangun datar bersisi tiga dan mempunyai tiga sudut yang jumlah besar ketiga sudut-sudutnya adalah 180^o. Bagaimanakah sepasang segitiga dapat dikatakan sebangun?

A. Segitiga-segitiga yang diketahui ukuran ketiga sisinya

Untuk lebih jelasnya kalian dapat mengamati animasi berikut. Pada bidang berpetak berikut terdapat gambar sepasang segitiga siku-siku yang diketahui ukuran ketiga sisinya, pada ∆ JKL sisi JK = 4 satuan dan JL = 3 satuan, dan pada ∆ STU sisi ST = 8 satuan dan SU = 6 satuan. Dapatkah kalian menunjukkan pasangan sisi-sisi yang bersesuaian dan menentukan perbandingan panjang sisi-sisi yang bersesuaian antara ∆JKL dan ∆ STU? Apakah ∆ JKL dan ∆ STU sebangun?

Pasangan sisi-sisi yang bersesuaian adalah:ST dengan JK, SU dengan JL dan TU dengan KL.
Perbandingan sisi-sisi tersebut adalah:
ST = 8 satuan = 2, SU = 6 satuan = 2, TU = 2 satuan = 2
JK 4satuan JL 3 satuan KL 5 satuan

Tahukah kalian, bagaimana mengetahui panjang TU = 10 satuan dan KL = 5 satuan? Benar, masih ingat teorema Pythagoras? Ya, dengan menggunakan teorema Pythagoras kalian dapat mengetahui panjang TU dan KL tersebut!

Perbandingan panjang sisi-sisi yang bersesuaian pada kedua segitiga ternyata sama atau senilai. Bagaimanakah dengan sudut-sudutnya? Klik kembali tombol play
Pada animasi dapat diamati ternyata sudut-sudut yang bersesuaian letaknya akan saling menempati atau berhimpit sehingga besar kedua sudut tersebut adalah sama besar.

Ð J menempati Ð S, maka Ð J = Ð S

Ð L menempati Ð U, maka Ð L = Ð U

Ð K menempati Ð T, maka Ð K = Ð T

Bagaimana kesimpulanmu setelah mengamati animasi tadi? Apakah kedua segitiga tersebut sebangun? Apa syarat kesebangunan untuk sepasang segitiga itu sudah terpenuhi meskipun hanya diketahui ukuran ketiga sisi-sisinya?
Ya, benar. Segitiga tersebut adalah sebangun meskipun hanya diketahui panjang ketiga sisi-sisinya . Dengan perbandingan panjang sisi-sisinya yang bersesuaian sama atau senilai, ternyata juga telah dibuktikan sudut-sudut yang bersesuaian pun ternyata juga sama besar.

Kesimpulan : Jika dua segitiga diketahui ketiga sisi-sisinya dan mempunyai perbandingan sisi-sisi yang bersesuaian sama atau senilai, maka dua segitiga tersebut adalah sebangun.

B. Segitiga-segitiga yang diketahui ketiga ukuran sudutnya.
Pada gambar berikut terdapat sepasang segitiga sebarang yang diketahui ukuran sudut-sudutnya. Sudut-sudut yang bersesuaian antara ∆ ABC dan ∆ PQR sama besar,yaitu ÐA = ÐP = 70^o, ÐB = ÐQ = 45^o dan ÐC = ÐR = 65^o. Menurut kalian, apakah ∆ ABC dan ∆ PQR sebangun? Untuk membuktikannya kalian amati animasi berikut ini. Kliklah pada tombol play!

Dengan menggunakan mistar, kalian dapat mengukur panjang setiap sisi pada kedua segitiga. Berdasarkan hasil pengukuran diperoleh hasil sebagai berikut:

Pada ∆ ABC, panjang AB = 20 cm, BC = 21 cm dan AC = 15 cm.
Pada ∆ PQR, panjang PQ = 18 cm, QR = 18,9 cm dan PR = 13,5 cm

Lalu coba kalian tentukan perbandingan panjang sisi-sisi yang bersesuaian. Sisi-sisi yang bersesuaian adalah AB dan PQ, BC dan QR, serta AC dan PR. Bisa kalian tentukan nilai perbandingannya? Ya, benar. Perbandingannya adalah:

AB = 20 cm = 1 1= 1,111, BC = 21 cm = 1,111 dan AC = 15 cm = 1,111
PQ 18 CM 9 QR 18,9cm PR 13,5cm

Ternyata perbandingan sisi-sisi yang bersesuaian memiliki perbandingan yang sama atau senilai. Maka dengan demikian ∆ ABC dan ∆ PQR sebangun.

Kesimpulan : Jika dua segitiga diketahui ukuran ketiga sudutnya dan ukuran sudut-sudut yang bersesuaian sama, maka dua segitiga tersebut adalah sebangun.

Bagaimana peserta didik sekalian? Sudah dapat memahami materi kesebangunan pada segitiga? Kita akan perdalam lagi dengan menyelesaikan beberapa masalah berikut ini.

Contoh 1 :

Perhatikan gambar. Diketahui ∆ ABC dengan < B = 40^o dan <C = 65^o. Pada ∆ PQR diketahui < Q = 75^o dan<R = 40^o. Tentukan:

a. Apakah ∆ ABC dan ∆ PQR sebangun?

b. Jika sebangun tuliskan perbandingan sisi-sisi bersesuaian yang senilai

Bagaimana menurutmu, apakah kedua segitiga itu sebangun?
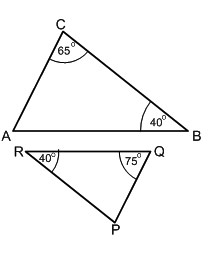
Dapatkah kalian menulisakan perbandingan sisi-sisi yang senilai?

Jawab :

a. Pada ∆ ABC, <B = 40^o dan < C = 65^o, maka besar

< A = 180^o – (40^o + 65^o)

= 180^o – 105^o

= 75^o

Pada ∆ PQR,< Q = 75^o dan< R = 40^o, maka besar

<P = 180^o – (75^o + 40^o)

= 180^o – 115^o

= 65^o

< A = < Q = 75^o, < B = < R = 40^o dan < C = < P = 65^o

Karena ketiga sudut pada kedua segitiga sama besar, maka ∆ ABC dan ∆ PQR sebangun.

b. Karena segitiga ABC dan segitiga PQR sebangun, maka perbandingan sisi-sisi yang bersesuaian akan senilai, yaitu:
AB = BC = AC
QR PR PQ

Contoh 2 :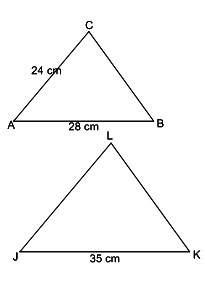

Pada gambar ∆ ABC dan ∆ JKL sebangun. Berapakah panjang sisi JL ?
Jawab :

Karena kedua segitiga sebangun maka mempunyai perbandingan sisi yang senilai.

Contoh 3 :

Pada gambar terdapat tiga buah segitiga siku-siku ∆ ABC, ∆ ABD dan ∆ ACD.
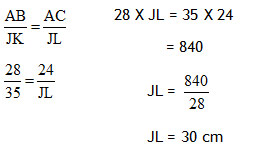
Dapatkah kalian menentukan pasangan segitiga-segitiga yang sebangun? Dan bagaimana membuktikannya?
1) Apakah ∆ABC dan ∆ABD sebangun?
2) Apakah ∆ABC dan ∆ ACD sebangun?
3) Apakah ∆ ABD dan ∆ ACD sebangun

Jawab :
1) Apakah ∆ ABC dan ∆ ABD sebangun?
Pembuktian ∆ ABC dan ∆ ABD sebangun adalah:
<BAC = <ADB (diketahui siku-siku)
<ABC =<ABD (diketahui berhimpit), maka
< ACB =< BAD
Dengan demikian ∆ABC dan ∆ABD sebangun.
Karena sebangun, maka perbandingan sisi-sisi yang bersesuaian akan senilai, yaitu:

AB = AC = BC ambil perbandingan dua sisi
BD AD AB

AB = BC dengan mengambil perkalian silang di peroleh
BD AB

AB x AB = BD x BC sehingga AB² = BD x BC

2) Apakah ∆ABC dan∆ ACD sebangun?
         Pembuktian  ABC dan  ACD sebangun adalah:
       < BAC =< ADC ( siku-siku)
          < ACB = < ACD (berhimpit), maka
        <ABC = <CAD
Dengan demikian ∆ ABC dan ∆ ACD sebangun.
Karena sebangun, maka perbandingan sisi-sisi yang bersesuaian akan senilai, yaitu:
AB = AC = BC ambil perbandingan dua sisi
AD    CD    AC
AC = BC dengan perkalian silang diperoleh
CD      AC
AC x AC = CD x BC sehingga
AC² = CD x CB

3) Apakah ∆ ABD dan ∆ ACD sebangun?
    Pembuktian ∆ABD dan ∆ ACD sebangun adalah:
Jika < B = x^odan < C = y^o, maka
< CAD = 180^o – 90^o- y^o
           = 90^o - y^o
< DAB = 180^o – 90^o- x^o
           = 90^o - x^o
< CAD + < DAB   = < CAB
90^o - y^o + 90^o - x^o = 90^o
       180^o – (y^o + x^o ) = 90^o
                 y^o + x^o   = 90^o
y^o   = 90^o - x^o   dan x^o = 90^o - y^o
y^o   = 90^o - x^o   -> < CAD = 90^o - y^o
                                     = 90^o – (90^o - x^o)
                                     = 90^o – 90^o + x^o
                                     = x^o
x^o   = 90^o - y^o   -> < DAB = 90^o - x^o
                                   = 90^o – (90^o - y^o)
                                   = 90^o – 90^o + y^o
                                   = y^o

< ADB = < ADC (diketahui siku-siku)
  < ABD = < CAD = x^o
   < DAB = < ACD = y^o
Dengan demikian ∆ ABD dan ∆ACD sebangun.
Karena sebangun, maka perbandingan sisi-sisi yang bersesuaian akan senilai, yaitu:
AB = DB = AD ambil perbandingan dua sisi DB = AD
AC    AD    DC                                          AD    DC
dengan perkalian silang didapat AD x AD = DB x DC atau AD² = DB x DC

Contoh 4 :

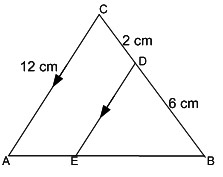
Pada gambar ∆ABC dengan DE // CA, diketahui panjang BD = 6 cm, DC = 2 cm dan CA = 12 cm. Hitunglah panjang DE.

Jawab :

∆ABC dan ∆ BED sebangun dengan syarat ketiga sudut yang bersesuaian sama besar terpenuhi, maka terdapat perbandingan sisi-sisi yang bersesuaian senilai, yaitu:

BD = DE
BC    CA
6    = DE
6+2     12
12 x 6 = DE x 8
    72   = 8.DE
   DE = 72 = 9 jadi panjang DE adalah 9cm
             8

Contoh 5 :

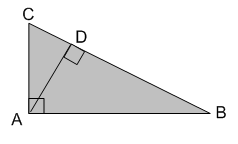
Perhatikan pada gambar ∆ ABC siku-siku di A. Panjang CD = 8 cm dan BC = 40 cm. Dapatkah kalian menentukan panjang AD?

Jawab :

Contoh 6 :

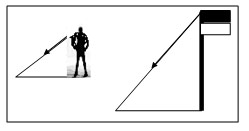
Pada gambar nampak bayangan tiang bendera saat terkena sinar matahari. Seseorang berdiri di dekat tiang tersebut dan membentuk bayangan di tanah sepanjang 2 m. Jika tinggi badan orang itu 160 cm, dapatkah kalian menentukan tinggi tiang bendera jika panjang bayangan tiang bendera itu 7 m?

Jawab :

Keadaan seperti di atas dapat disketsakan sebagai pasangan segitiga siku-siku yang sebangun.
Terdapat perbandingan senilai :

tinggi tiang bendera = panjang bayangan tiang
tinggi badan orang      panjang bayangan orang
t         = 7m
160cm      2m
t          =   7
160          2
2t        = 7 x 160
2t        = 7 x 160
2t        = 1.120
t         = 1.120
                 2
t          = 560
Jadi tinggi tiang bendera adalah 560cm atau 5,6 m