2. Garis dengan gradien m dan melalui 1 titik

Perhatikan gambar dibawah ini !

 

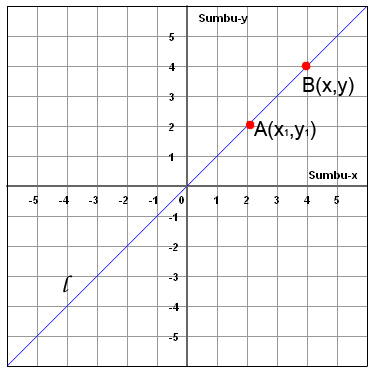
Pada garis l terdapat titik A dengan koordinat (x₁, y₁) dan titik B dengan koordinat bebas, yaitu (x , y), bila gradien garis l dinyatakan dengan m, maka AB terdiri atas semua titik (x,y) dengan hubungan berikut ini :

y - y₁ = m (x - x₁)

 

Kesimpulan :

Persamaan garis dengan gradien m dan melalui sebuah titik (x₁ , y₁), adalah :

y - y₁ = m (x - x₁)

 

Contoh 1 :

Tentukanlah persamaan garis melalui titik A(-3,4) dan bergradien -2.

Penyelesaian :

Titik A(-3,4), berarti x­1 = -3 , y₁ = 4 dan bergradien -2, berarti m = -2

Persamaan garis dengan gradient m dan melalui sebuah titik (x₁,y₁) adalah :

y - y₁ = m ( x - x₁ )

y - 4 = -2 {x - (-3)}

y - 4 = -2 (x + 3 )

y - 4 = -2 x - 6

y = -2x - 6 + 4

y = -2x - 2

Jadi persamaan garis melalui titik A(-3,4) dan bergradien -2 adalah y = -2x - 2

Contoh 2 :

Tentukanlah persamaan garis melalui titik B(6,2) dan sejajar dengan garis yang melalui titik P(2,-5) dan Q(-6, 3)

 

Penyelesaian :

Garis yang melalui titik P(2,-5) dan (-6, 3)

P(2,-5) berarti x₁ = 2 , y₁ = -5

Q(-6,3) berarti x₂ = -6 , y₂ = 3

Gradien yang melaui titik P(2,-5) dan Q(-6, 3) adalah m_PQ

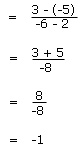
Misal m_PQ = m₁, maka m₁ = m₂ = -1 ( dua garis sejajar )

Titik B(6, 2), berarti x­1 = 6 , y₁ = 2

Persamaan garis dengan gradien -1 dan melalui titik (6, 2) adalah :

y - y₁ = m ( x - x₁ )

y - 2 = -1 (x - 6)

y - 2 = -x + 6

y = -x + 6 + 2

y = -x + 8

 

Jadi persamaan garis melalui titik B(6,2) dan bergradien -1 adalah y = -x + 8

 

---