Untuk memahami pertidaksamaan linier satu variabel, perhatikan gambar berikut:

 

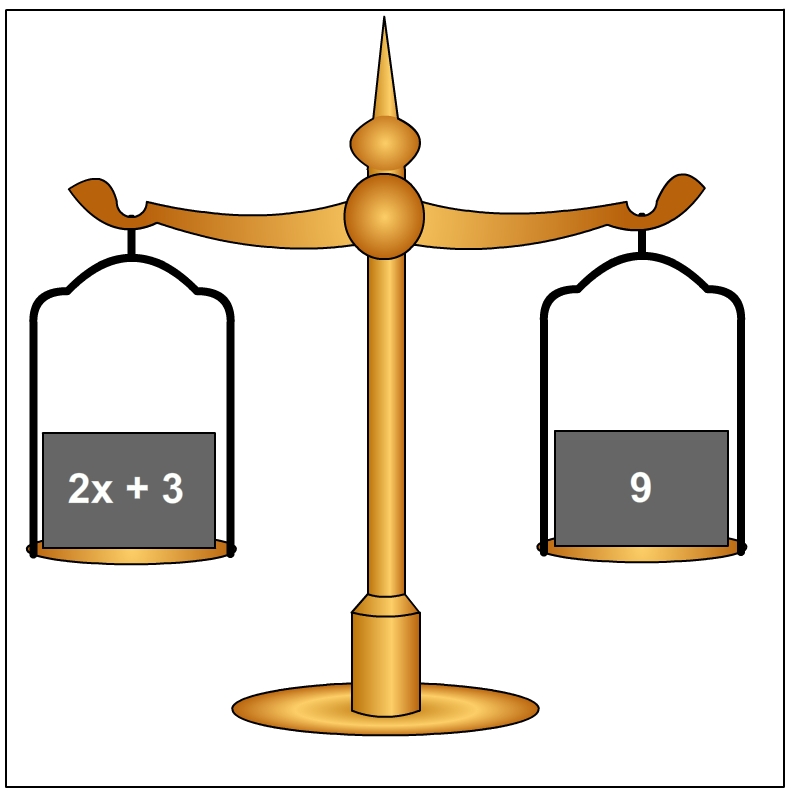
Gambar 1 : menunjukkan persamaan 2x + 3 = 9

 

 

Gambar 2 : menunjukkan pertidaksamaan 2x + 3 > 9

 

 

 

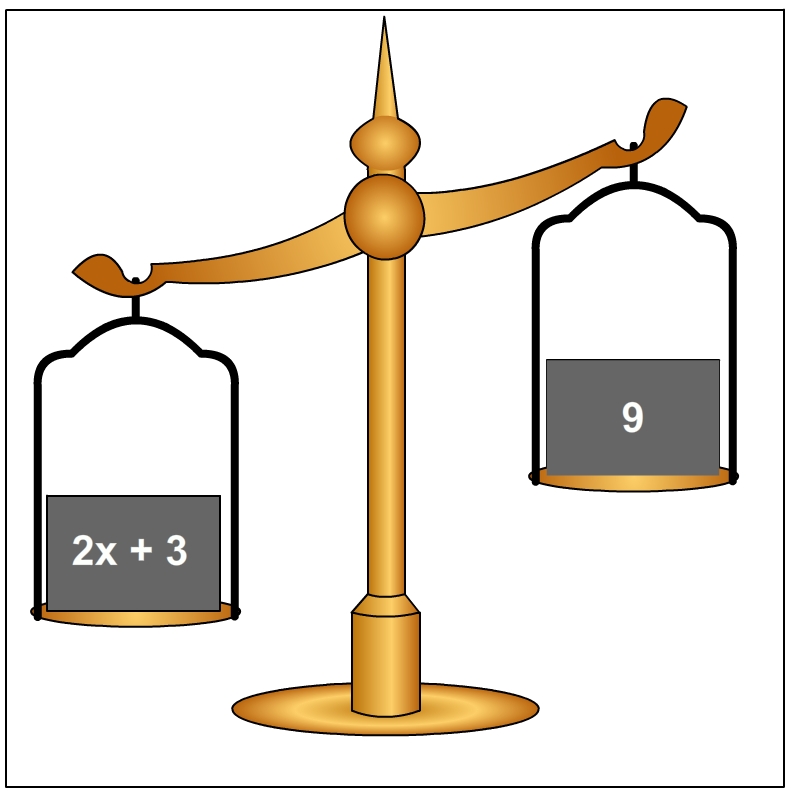
Pada bentuk 2x + 3 > 9

• 2 pada 2x, dinamakan koefisien
• x pada 2x, dinamakan variabel/peubah
• 3 dan 9 , dinamakan konstanta
• Jadi 2x + 3 > 9 adalah pertidaksamaan linier satu variabel

 

Bentuk lain dari pertidaksamaan linier satu variabel adalah:

1. ax < b, misalnya 2x < 4
2. ax ± b ≥ c, misalnya 2x – 3 ≥ 7
3. ax ± b ≤ cx ± d, misalnya 3x – 4 ≤ x + 2
4. a(x ± b) > c(x ± d), misalnya 2(x – 1) > 3 (x + 6)
5. dan sebagainya

 

Dari contoh tersebut dapat diambil kesimpulan bahwa pertidaksamaan linier satu variabel adalah kalimat terbuka dengan satu variabel berpangkat satu yang dihubungkan dengan tanda ketidaksamaan.

 

Lambang ketidaksamaan adalah:

1. kurang dari, ditulis “ < “
2. lebih dari, ditulis “ > “
3. kurang dari atau sama dengan, ditulis “ ≤ “
4. lebih dari atau sama dengan, ditulis “ ≥ “

 

Bagaimanakah cara menentukan penyelesaian 3x – 1 < x + 3 ?

 

Perhatikan langkah-langkah berikut:

 

3x – 1 < x + 3

⇔ 3x – 1 + 1 < x + 3 + 1 ......kedua ruas ditambah dengan 1

 

⇔ 3x < x + 4

⇔ 3x – x < x + 4 – x .............kedua ruas dikurang dengan x

 

⇔ 2x < 4

⇔ 2x : 2 < 4 : 2 ...................kedua ruas dibagi dengan 2

 

⇔ x < 2

Jadi penyelesaian 3x – 1 < x + 3 adalah x < 2

 

Suatu pertidaksamaan dapat dinyatakan ke dalam pertidaksamaan yang ekuivalen dengan cara sebagai berikut:

1. menambah atau mengurangi kedua ruas dengan bilangan yang sama tanpa mengubah tanda ketidaksamaan.
2. Mengalikan atau membagi kedua ruas dengan bilangan positif yang sama tanpa mengubah tanda ketidaksamaan.
3. Mengalikan atau membagi kedua ruas dengan bilangan negatif yang sama dengan mengubah tanda ketidaksamaan, yaitu:

 

1.  “ > “ menjadi “ < “
2. “ < “ menjadi “ > “
3. “ ≥ “ menjadi “ ≤ “
4. “ ≤ “ menjadi “ ≥ “