Kompetensi

Materi

 

 

 

Latihan

Simulasi

 

 

Tes

Tim

 

Deret Aritmetika dan Geometri

 

Deret Aritmetika

Apabila barisan bilangan aritmetika dijumlahkan maka akan terbentuk deret Aritmetika
Contoh :
Barisan Aritmetika : 2, 6 , 10 , 14 , ... .
Deret Aritmetika : 2 + 6 + 10 + 14 + ... .
Jumlah n suku pertama deret aritmetika ditulis dengan Sn
Jadi S1 = U1 = 2
       S2 = U1 + U2 = 2 + 6 = 8
       S3 = U1 + U2 + U3 = 2 + 6 + 10 = 18
       S4 = U1 + U2 + U3 + U4 = 2 + 6 + 10 + 14 = 32
       .....
       Sn = U1 + U2 + U3 + ... + Un
 
Rumus jumlah n suku pertama deret aritmetika
Sn = U1 +    U2      +     U3     + ... + Un
Sn =  a + (a + b)  + (a + 2b) + ... + Un
Sn = Un + Un - b    + Un – 2b  + ... + a
----------------------------------------------- +
2.Sn = (a + Un) + (a + Un) + ... + (a +Un)
2.Sn = n (a + Un)

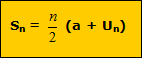 , karena Un = a + (n-1)b, maka Sn = (a + Un)
  atau  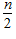                                                                  = (a + a + (n-1) b )
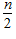                                                                            = (2a + (n – 1) b)
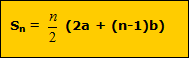
dengan Sn = jumlah n suku pertama
             a  = suku awal
             b  = beda      
 
 
Contoh :

Jumlah dari  100 + 95 + 90 + 85 + ... + 5 = ...

Jawaban :

a = 100
b = 95 – 100
   = 90 – 95
   = -5

Un = a + (n-1)b
  5 = 100 + (n-1)(-5)
95 = (n-1)(-5)
19 = (n-1)
  n = 20
 
Sn = 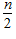(2a + (n – 1) b)
S20 = 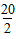(2x100 + (20 – 1)(-5))
       =10 (200 - 95)
       =10 (105)
       =1050
   
Jadi jumlah dari 100 + 95 + 90 + 85 + ... + 5 = 1.050
 
 
 
Deret Geometri

Apabila barisan bilangan geometri dijumlahkan maka akan terbentuk deret geometri
Contoh :
Barisan geometri : 2, 6 , 18 , 54 , ... .
Deret geometri : 2 + 6 + 18 + 54 + ... .
Jumlah n suku pertama deret aritmetika ditulis dengan Sn
Jadi S1 = U1 = 2
       S2 = U1 + U2 = 2 + 6 = 8
       S3 = U1 + U2 + U3 = 2 + 6 + 18 = 26
       S4 = U1 + U2 + U3 + U4 = 2 + 6 + 18 + 54 = 80
       ...
       
      
Rumus jumlah n suku pertama deret geometri
        Sn = U1 +    U2     +     U3     + ... + Un

        Sn =  a +   (ar)    +    (ar2)   +  ... + arn-1
   r x Sn =          (ar)     +    (ar2)   + .... + arn-1  + arn 
 -
Sn– r.Sn =  a   +    0       +     0      +       +   0    + arn
(1 – r)Sn = a                                                      – arn
(1 – r)Sn = a (1 – rn)
 
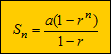 untuk nilai r < 1, atau 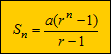, untuk r > 1
 
dengan Sn = jumlah n suku pertama
             a  = suku awal                                                        
             r  = rasio                                                         
                                                        
 
                                             
Contoh :
   Jumlah dari  400 + 200 + 100 + 50 + 25 + 12,5 = ...
                                                        

Jawaban :
   a = 400
    r = 200 : 400
                                                        
      = 100 : 200
                                                        
      = ½
    n = 6

                                                         
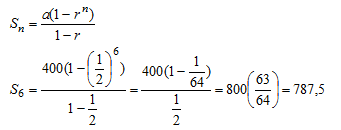
Jadi jumlah dari 500 + 200 + 100 + 50 + 25 + 12,5 = 787,5