 |
 |
Perbandingan
Kegiatan Belajar 3
Perbandingan Berbalik Nilai
Kalian telah memahami perbandingan senilai, lantas bagaimana dengan konsep perbandingan berbalik nilai? Perhatikan ilustrasi berikut.
Ibu Siti membeli sekaleng coklat untuk dibagikan kepada 6 orang muridnya secara merata. Jika 6 orang muridnya datang semua maka masing-masing akan menerima 10 biji.
Berapakah isi coklat dalam kaleng?
Jika murid yang datang 5 orang, berapakah masing-masing mendapatkan coklat?
Jika murid yang datang 4 orang, berapakah coklat yang diterima?
Jika murid yang datang 3 orang, berapakah coklat yang diterima?
Masalah tersebut dapat kalian lihat pada tabel:

Perhatikan bahwa jika murid yang datang makin banyak maka coklat yang diterima masing-masing makin sedikit
Ini adalah permasalahan perbandingan berbalik nilai.
Setelah kalian memahami konsep perbandingan berbalik nilai, lantas bagaimanakah menyelesaikan masalah perbandingan berbalik nilai?
Masalah perbandingan berbalik nilai dapat diselesaikan dengan:
1. Perhitungan berdasarkan hasil kali
Perhatikan tabel baris ke-2 dan ke-5

Perhatikan bahwa hasil perkalian bilangan pada setiap baris selalu sama.
2 x 30 = 5 x 12
Contoh berikut akan menunjukkan perhitungan dengan hasil kali.
2 lusin pensil akan diberikan kepada 6 orang siswa secara merata, jika pensil tersebut akan dibagikan kepada 4 orang siswa, maka berapakah pensil yang diterima masing-masing siswa?
Persoalan tersebut dapat diselesaikan sebagai berikut:
Banyak pensil = 2 lusin = 24 batang, banyak siswa = 6 orang, sehingga masing-masing akan menerima 24 : 6 = 4 batang pensil.
6 orang ⟶ 4 batang pensil
4 orang ⟶ p batang pensil
hasil perkalian antar baris sama, maka 6 x 4 = 4 x p ⟶ p = 4x6 = 6
4
Jadi pensil yang diterima masing-masing siswa adalah 6 batang
1. Perhitungan berdasarkan perbandingan
Perhatikan tabel baris ke 2 dan ke 5
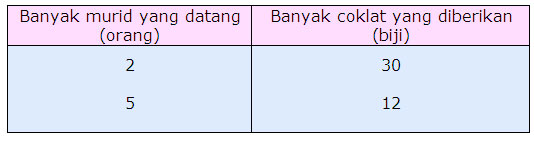
Perhatikan bahwa hasil perbandingan kolom pertama sama dengan hasil kebalikan perbandingan pada kolom kedua.
2 = 12
5 30
Contoh berikut akan menunjukkan perhitungan berdasarkan perbandingan.
Dua lusin pensil akan diberikan kepada 6 orang siswa secara merata, jika pensil tersebut akan dibagikan kepada 4 orang siswa, maka berapakah pensil yang diterima masing-masing siswa?
Masalah tersebut dapat diselesaikan, yaitu:
Banyak pensil = 2 lusin = 24 batang, banyak siswa = 6 orang, sehingga masing-masing akan menerima 24 : 6 = 4 batang pensil.
6 orang ⟶ 4 batang pensil
4 orang ⟶ p batang pensil
Perbandingan antar kolom:
6 - p ⟹ 6 x 4 = 4 x p ⟶ p = 4x6 = 6
4 4 4
Jadi pensil yang diterima masing-masing siswa adalah 6 batang
Kalian telah memahami perbandingan senilai, lantas bagaimana dengan konsep perbandingan berbalik nilai? Perhatikan ilustrasi berikut.
Ibu Siti membeli sekaleng coklat untuk dibagikan kepada 6 orang muridnya secara merata. Jika 6 orang muridnya datang semua maka masing-masing akan menerima 10 biji.
Berapakah isi coklat dalam kaleng?
Jika murid yang datang 5 orang, berapakah masing-masing mendapatkan coklat?
Jika murid yang datang 4 orang, berapakah coklat yang diterima?
Jika murid yang datang 3 orang, berapakah coklat yang diterima?
Masalah tersebut dapat kalian lihat pada tabel:

Perhatikan bahwa jika murid yang datang makin banyak maka coklat yang diterima masing-masing makin sedikit
Ini adalah permasalahan perbandingan berbalik nilai.
Setelah kalian memahami konsep perbandingan berbalik nilai, lantas bagaimanakah menyelesaikan masalah perbandingan berbalik nilai?
Masalah perbandingan berbalik nilai dapat diselesaikan dengan:
1. Perhitungan berdasarkan hasil kali
Perhatikan tabel baris ke-2 dan ke-5

Perhatikan bahwa hasil perkalian bilangan pada setiap baris selalu sama.
2 x 30 = 5 x 12
Contoh berikut akan menunjukkan perhitungan dengan hasil kali.
2 lusin pensil akan diberikan kepada 6 orang siswa secara merata, jika pensil tersebut akan dibagikan kepada 4 orang siswa, maka berapakah pensil yang diterima masing-masing siswa?
Persoalan tersebut dapat diselesaikan sebagai berikut:
Banyak pensil = 2 lusin = 24 batang, banyak siswa = 6 orang, sehingga masing-masing akan menerima 24 : 6 = 4 batang pensil.
6 orang ⟶ 4 batang pensil
4 orang ⟶ p batang pensil
hasil perkalian antar baris sama, maka 6 x 4 = 4 x p ⟶ p = 4x6 = 6
4
Jadi pensil yang diterima masing-masing siswa adalah 6 batang
1. Perhitungan berdasarkan perbandingan
Perhatikan tabel baris ke 2 dan ke 5

Perhatikan bahwa hasil perbandingan kolom pertama sama dengan hasil kebalikan perbandingan pada kolom kedua.
2 = 12
5 30
Contoh berikut akan menunjukkan perhitungan berdasarkan perbandingan.
Dua lusin pensil akan diberikan kepada 6 orang siswa secara merata, jika pensil tersebut akan dibagikan kepada 4 orang siswa, maka berapakah pensil yang diterima masing-masing siswa?
Masalah tersebut dapat diselesaikan, yaitu:
Banyak pensil = 2 lusin = 24 batang, banyak siswa = 6 orang, sehingga masing-masing akan menerima 24 : 6 = 4 batang pensil.
6 orang ⟶ 4 batang pensil
4 orang ⟶ p batang pensil
Perbandingan antar kolom:
6 - p ⟹ 6 x 4 = 4 x p ⟶ p = 4x6 = 6
4 4 4
Jadi pensil yang diterima masing-masing siswa adalah 6 batang
![]()